Research
My main field of research is the the numerical analysis and simulation of PDEs, with a particular interest for problems arising from electronic structure theory and quantum chemistry / physics. My work can be summarized in two main aspects:
the numerical analysis of existing methods in electronic structure calculations, in order to understand the behavior of the algorithms and discretization methods that are used in practice,
the development of new numerical methods, whether to estimate different sources of errors arising in numerical simulations or to improve the efficiency of existing methods.
Supervision
Taha Bamhaoute, Estimation d’erreur et optimisation de méthodes numériques pour la théorie de la fonctionnelle de densité (juin - septembre 2024, stage M1 Matmeca, Bordeaux INP, avec Jean-Paul Chehab).
Research (detailled)
Numerical analysis of methods and algorithms used in electronic structure calculations
In the past decades, more and more applied mathematiciens got interested into analyzing the numerical methods used by chemists and physicists in electronic structure calculations. Indeed, most of the problems arising in these fields can be reformulated as nonlinear eigenproblems: applied mathematics can thus bring new insights on the convergence of numerical methods, or even improve the existing ones, and there is still a lot to do and understand!
In my first work on such algorithms, we analyzed, in a common mathematical framework, two classes of methods that are a priori different: direct minimization and self-consistent field (SCF) algorithms. This enables for instance to understand, from a mathematical point of view, the influence of small spectral gaps on the convergence of SCF algorithms. The analysis is based on a linearization of the problem that can also be used to understand the relation between residuals (that we can compute) and discretization errors (that we want but cannot be computed).
More recently, I also worked on the convergence of the discretized solutions to linear and nonlinear periodic Schrödinger equations for a specific class of analytic potentials. By introducing Hardy-like spaces, we are able to show the exponential convergence with respect to the discretization parameters.
Related works:
E. Cancès, G. Kemlin, and A. Levitt. A priori error analysis of linear and nonlinear periodic Schrodinger equations with analytic potentials. Journal of Scientific Computing, 98(1):25, 2024. doi - pdf
E. Cancès, G. Dusson, G. Kemlin, and L. Vidal. On basis set optimisation in quantum chemistry. ESAIM: ProcS, 73:107-129, 2023. doi - pdf
E. Cancès, G. Kemlin, and A. Levitt. Convergence analysis of direct minimization and self-consistent iterations. SIAM Journal on Matrix Analysis and Applications, 42(1):243-274, 2021. doi - pdf
Error control and post-processing techniques in plane-wave density functional theory
Another important topic at the moment in electronic structure calculations is the estimation of errors, which can be of different sources, among which we can list:
modelling error, coming from the approximation of the -body Schrödinger equation, fully known but way too complicated to be solved for real systems, by different models (e.g. Hartree-Fock, Kohn-Sham DFT, Gross-Pitaevskii, Coupled Cluster...);
discretization error, coming from the numerical approximation of the continuous equations given by the chosen model;
algorithmic error, coming from the resolution of the discretized equations.
Again, there is a lot to do in these topics for applied mathematicians. For instance, regarding the discretization error, there is a judgemental litterature on the topic for linear PDEs and eigenproblems, but there is much fewer results regarding nonlinear elliptic eigenproblems that are at the heart of electronic structure calculations. In my first works on these topics, we could propose efficient error estimates for nonlinear Kohn-Sham models. However, the strategy being based on the linearization of the underlying equations, such bounds are not guaranteed. We observed that they were still very useful in practice, with some mathematical justification in specific cases.
At the moment, with additional insights from works in progress, my understanding of the problem is that fully guaranted error estimates for nonlinear elliptic eigenproblems are either very expensive or too coarse to be used in practice. All hope is not gone as it is still possible to obtain efficient estimators if the guaranted constrainted is relaxed.
Note that getting an estimate of the error on some quantity is not the goal per se: such estimates can often be used in a post-processing calculations to enhance the accuracy too.
Related works:
A. Bordignon, E. Cancès, G. Dusson, G. Kemlin, R.A. Lainez Reyes, B. Stamm. Fully guaranteed and computable error bounds on the energy for periodic Kohn-Sham equations with convex density functionals. SIAM Journal on Scientific Computing, 47(5):A2881-A2905, 2025. doi - pdf
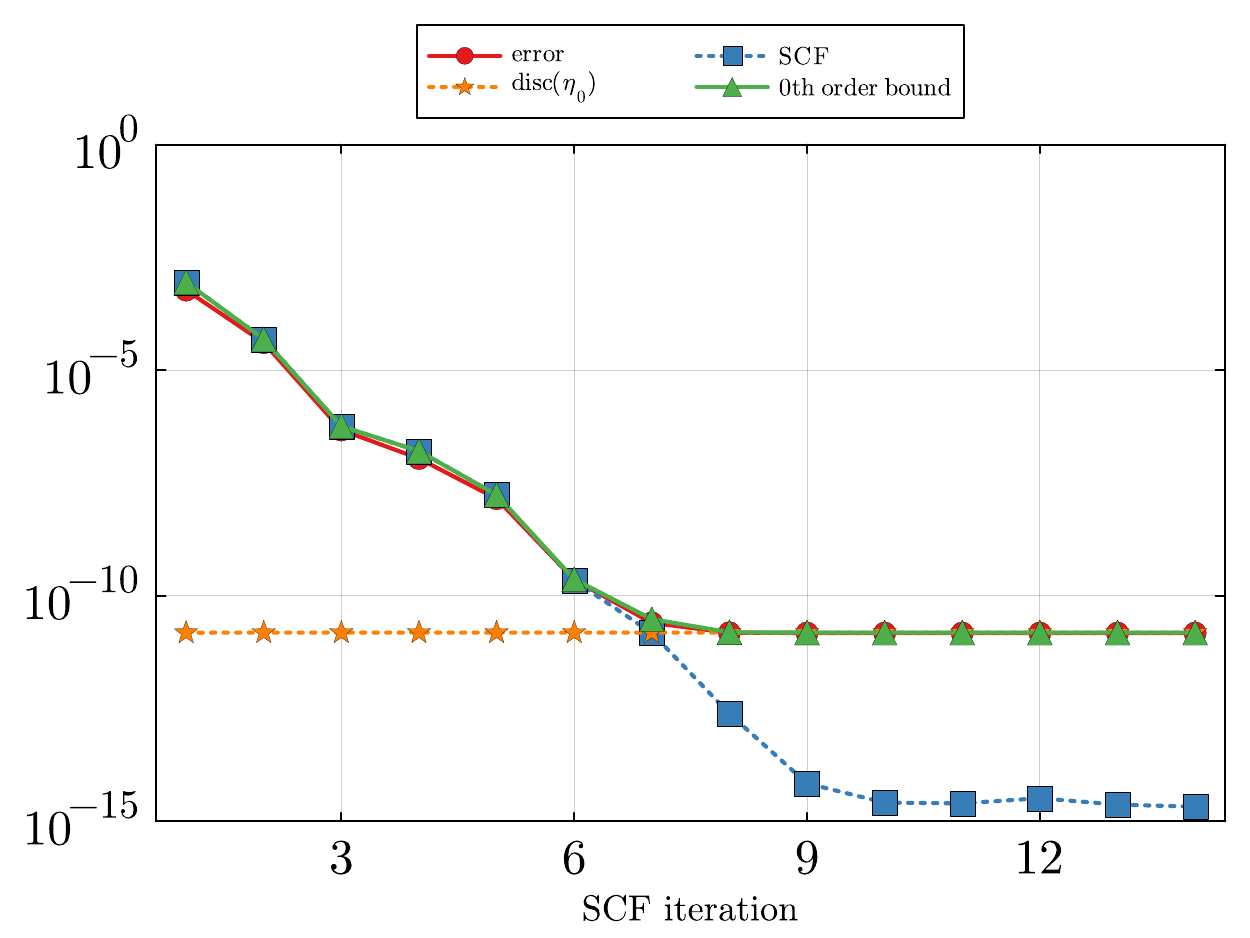 Error bounds on the energy for Kohn-Sham equations with convex
density functionals, with a splitting between discretization and SCF (fixed
point iterations) contributions.
Error bounds on the energy for Kohn-Sham equations with convex
density functionals, with a splitting between discretization and SCF (fixed
point iterations) contributions.
E. Cancès, M. F. Herbst, G. Kemlin, A. Levitt, and B. Stamm. Numerical stability and efficiency of response property calculations in density functional theory. Letters in Mathematical Physics, 113(1):21, 2023. doi - pdf
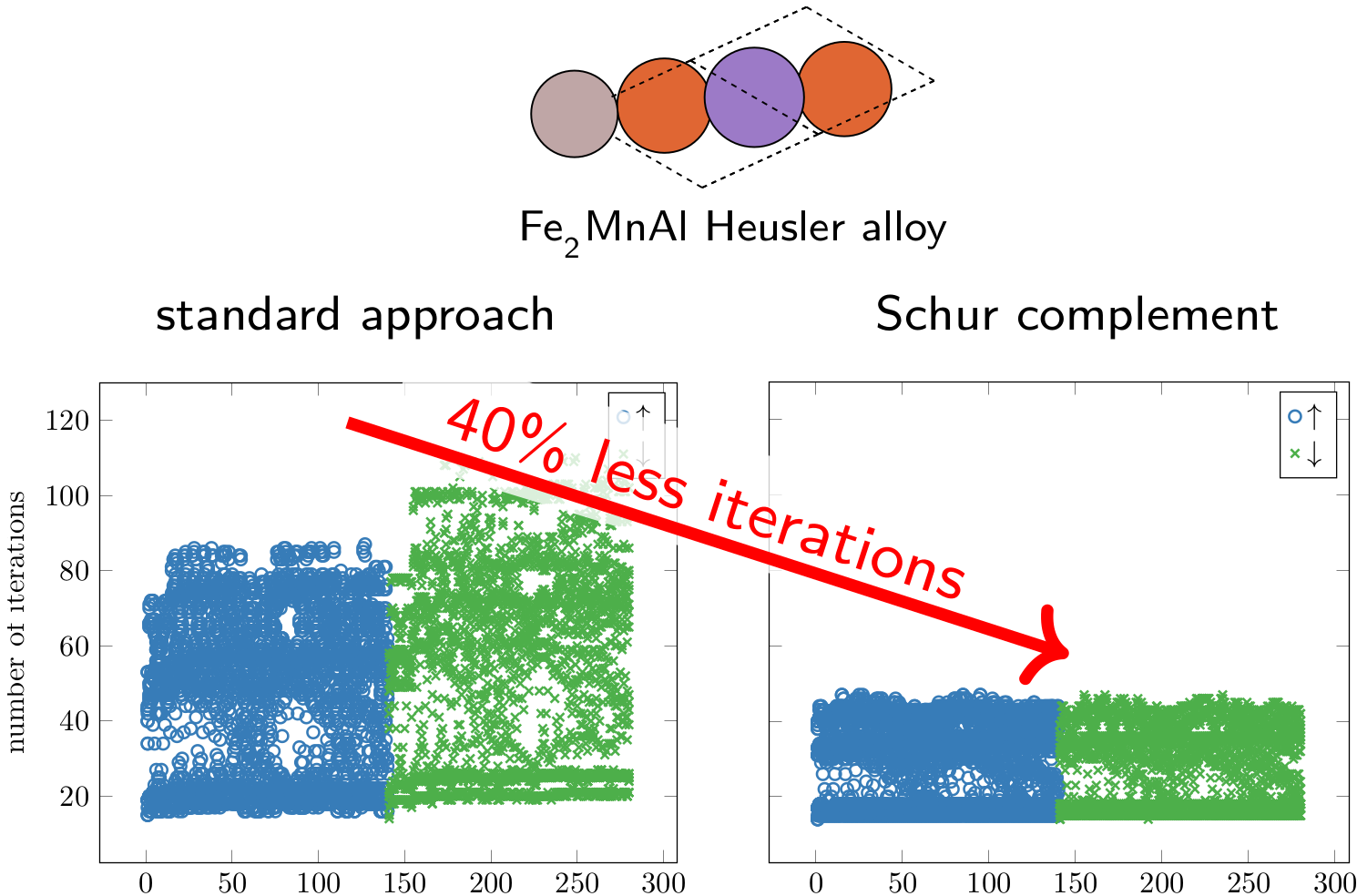 Response calculations for a Heusler alloy
(image from Michael F. Herbst).
Response calculations for a Heusler alloy
(image from Michael F. Herbst).
E. Cancès, G. Dusson, G. Kemlin, and A. Levitt. Practical error bounds for properties in plane-wave electronic structure calculations. SIAM Journal on Scientific Computing, 44(5):B1312-B1340, 2022. doi - pdf
Vortex-tracking for the Gross-Pitaevskii equation
A well-known feature of Gross-Pitaevskii-type equations is the appearance of quantized vortices with core size of the order of a small parameter . These vortices interact, in the singular limit , through an explicit Hamiltonian dynamics. Using this analytical framework, we can develop numerical strategies based on the reduced-order Hamiltonian system to efficiently simulate the infinite dimensional equation for small, but finite, . This allows to avoid numerical stability issues in solving such equations, where small values of typically require very fine meshes and time steps.
You can find some funny-looking simulations for the Gross-Pitaevskii equation
on the unit disc in and . Note that they were obtained within a few seconds on a laptop, a significant improvement regarding standard method in the regime of very small vortices! (+ / - stands for a vortex with positive / negative degree)
As for the magnetic Ginzburg-Landau equation, we developed a similar strategy with which we could obtain very nice simulations:
The previous simulations were obtained from the Schrödinger flow, which is known to preserve energy. Adding some dissipation, we can force to vortices to arrange into some stable pattern if the external magnetic field is strong enough:
Related works:
T. Carvalho Corso, G. Kemlin, C. Melcher and B. Stamm. Simulation of the magnetic Ginzburg-Landau equation via vortex tracking. pdf
T. Carvalho Corso, G. Kemlin, C. Melcher and B. Stamm. Numerical simulation of the Gross-Pitaevskii equation via vortex tracking. Mathematics of Computation, 95:227-262, 2026. doi - pdf
Domain decomposition methods
During my Master studies, I also worked on domain decomposition methods for the linearized Boussinesq equations in coastal oceanography.
Related works:
J. G. Caldas Steinstraesser, G. Kemlin, and A. Rousseau. A domain decomposition method for linearized Boussinesq-type equations. Journal of Mathematical Study, 52(3):320-340, 2019. doi - pdf
CC BY-SA 4.0 Gaspard Kemlin. Last modified: December 19, 2025.
Website built with Franklin.jl, the Hyde theme and the Julia programming language.